На букву К Со слова «комплексные»
Фраза «комплексные числа»
Фраза состоит из двух слов и 16 букв без пробелов.
- Синонимы к фразе
- Написание фразы наоборот
- Написание фразы в транслите
- Написание фразы шрифтом Брайля
- Передача фразы на азбуке Морзе
- Произношение фразы на дактильной азбуке
- Остальные фразы со слова «комплексные»
- Остальные фразы из 2 слов

Математика без Ху%!ни. Комплексные числа, часть 1. Введение.

Комплексные числа #1

Комплексные числа — Неизбежность (русский клип)

10 класс, 32 урок, Комплексные числа и арифметические операции над ними

Комплексные числа. Введение | Ботай со мной #039 | Борис Трушин ||

2016_04_26 — 35, 36 лек. А.В.Савватеева — Комплексные числа ч. 1/2
Синонимы к фразе «комплексные числа»
Какие близкие по смыслу слова и фразы, а также похожие выражения существуют. Как можно написать по-другому или сказать другими словами.
Фразы
- + алгебра логики −
- + алгебраическое многообразие −
- + бесконечно малая величина −
- + вариационное исчисление −
- + вещественное число −
- + гравитационная постоянная −
- + действительные числа −
- + десятичная дробь −
- + закон кратных отношений −
- + извлечение корня −
- + иррациональное число −
- + квант действия −
- + комплексная плоскость −
- + комплексные числа −
- + конечное число −
- + метод наименьших квадратов −
- + мнимая единица −
- + мнимые числа −
- + мысленный эксперимент −
- + натуральное число −
- + нормальное распределение −
- + однородный многочлен −
- + определённый интеграл −
- + правильный многоугольник −
Ваш синоним добавлен!
Написание фразы «комплексные числа» наоборот
Как эта фраза пишется в обратной последовательности.
алсич еынскелпмок 😀
Написание фразы «комплексные числа» в транслите
Как эта фраза пишется в транслитерации.
в армянской🇦🇲 կոմպլեկսնըե չիսլա
в грузинской🇬🇪 კომპლეკსნიე ჩისლა
в латинской🇬🇧 kompleksnye chisla
Как эта фраза пишется в пьюникоде — Punycode, ACE-последовательность IDN
xn--e1aanbdfkdkx5i xn--80apjx2a
Как эта фраза пишется в английской Qwerty-раскладке клавиатуры.
rjvgktrcystxbckf
Написание фразы «комплексные числа» шрифтом Брайля
Как эта фраза пишется рельефно-точечным тактильным шрифтом.
⠅⠕⠍⠏⠇⠑⠅⠎⠝⠮⠑⠀⠟⠊⠎⠇⠁
Передача фразы «комплексные числа» на азбуке Морзе
Как эта фраза передаётся на морзянке.
– ⋅ – – – – – – ⋅ – – ⋅ ⋅ – ⋅ ⋅ ⋅ – ⋅ – ⋅ ⋅ ⋅ – ⋅ – ⋅ – – ⋅ – – – ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ – ⋅ ⋅ ⋅ –
Произношение фразы «комплексные числа» на дактильной азбуке
Как эта фраза произносится на ручной азбуке глухонемых (но не на языке жестов).
Передача фразы «комплексные числа» семафорной азбукой
Как эта фраза передаётся флажковой сигнализацией.
Остальные фразы со слова «комплексные»
Какие ещё фразы начинаются с этого слова.
- комплексные задачи
- комплексные заклинания
- комплексные занятия
- комплексные исследования
- комплексные мероприятия
- комплексные меры
- комплексные органические удобрения
- комплексные отрасли
- комплексные препараты
- комплексные сети
- комплексные соединения
- комплексные углеводы
- комплексные удобрения
- комплексные упражнения
- комплексные услуги
Ваша фраза добавлена!
Остальные фразы из 2 слов
Какие ещё фразы состоят из такого же количества слов.
- а вдобавок
- а вдруг
- а ведь
- а вот
- а если
- а ещё
- а именно
- а капелла
- а каторга
- а ну-ка
- а приятно
- а также
- а там
- а то
- аа говорит
- аа отвечает
- аа рассказывает
- ааронов жезл
- аароново благословение
- аароново согласие
- аб ово
- абажур лампы
- абазинская аристократия
- абазинская литература
Комментарии

07:30
Что значит фраза «комплексные числа»? Как это понять?..
Ответить

02:13

×
Здравствуйте!
У вас есть вопрос или вам нужна помощь?
Спасибо, ваш вопрос принят.
Ответ на него появится на сайте в ближайшее время.
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я
Транслит Пьюникод Шрифт Брайля Азбука Морзе Дактильная азбука Семафорная азбука
Палиндромы Сантана

Народный словарь великого и могучего живого великорусского языка.
Онлайн-словарь слов и выражений русского языка. Ассоциации к словам, синонимы слов, сочетаемость фраз. Морфологический разбор: склонение существительных и прилагательных, а также спряжение глаголов. Морфемный разбор по составу словоформ.
По всем вопросам просьба обращаться в письмошную.
-
Определение комплексного числа.
Начать изучение
-
Свойства операций.
Начать изучение
-
Геометрическая интерпретация комплексного числа.
Начать изучение
-
Комплексная плоскость.
Начать изучение
-
Геометрический смысл модуля комплексного числа.
Начать изучение
-
Тригонометрическая и показательная формы комплексного числа.
Начать изучение
-
Извлечение корня.
Начать изучение
-
Комплекснозначные функции действительного переменного.
Начать изучение
Известно, что квадратное уравнение с вещественными коэффициентами и отрицательным дискриминантом не имеет вещественных корней. В частности, уравнение
$$
z^2+1=0nonumber
$$
не имеет корней на множестве (mathbb{R}). Возникает потребность расширить множество (mathbb{R}) так, чтобы на более широком множестве было разрешимо квадратное уравнение с любыми вещественными коэффициентами.
Определение комплексного числа.
Комплексными числами называют пары ((x,y)) вещественных (действительных) чисел (x) и (y), для которых следующим образом определены понятие равенства и операции сложения и умножения.
Обозначим комплексное число ((x,y)) буквой (z), то есть положим (z=(x,y)). Пусть (z_1=(x_1,y_1)), (z_2=(x_2,y_2)). Два комплексных числа (z_1) и (z_2) считаются равными тогда и только тогда, когда (x_1=x_2) и (y_1=y_2), то есть
$$
{(x_1,y_1) = (x_2,y_2)}Leftrightarrow {x_1=x_2} wedge {y_1 = y_2}.nonumber
$$
Сумма и произведение комплексных чисел (z_1) и (z_2) обозначаются соответственно (z_1+z_2) и (z_1z_2) и определяются формулами
$$
z_1+z_2=(x_1+x_2,y_1+y_2),label{ref1}
$$
$$
z_1z_2=(x_1x_2-y_1y_2,x_1y_2+x_2y_1).label{ref2}
$$
Из формул eqref{ref1} и eqref{ref2} следуют соотношения
$$
(x_1,0) + (x_2,0) = (x_1+x_2,0),qquad (x_1,0)(x_2,0) = (x_1x_2,0),nonumber
$$
которые показывают, что операции над комплексными числами вида ((x, 0)) совпадают с операциями над действительными числами. Поэтому комплексное число вида ((x, 0)) отождествляют с действительным числом (x), то есть полагают ((x,0) = x).
Среди комплексных чисел особую роль играет число ((0,1)), которое называют мнимой единицей и обозначают (i), то есть
$$
i = (0,1).nonumber
$$
Вычислив произведение (i) на (i) по формуле eqref{ref2}, получим
$$
icdot i = (0,1)(0,1) = (-1,0) = -1,nonumber
$$
то есть (i^2 = -1). Используя формулы eqref{ref1}, eqref{ref2}, находим
$$
icdot y = (0,1)(y,0) = (0,y),qquad (x,y) = (x, 0) + (0,y) = x + iy.nonumber
$$
Следовательно, любое комплексное число (z= (x,y)) можно записать в виде (x + iy), то есть
$$
z = x + iy.label{ref3}
$$
Запись комплексного числа (z = (x,y)) в виде eqref{ref3} называют алгебраической формой комплексного числа.
В записи eqref{ref3} число (x) называют действительной частью комплексного числа и обозначают (Re z), а число (y) — мнимой частью и обозначают (Im z), то есть
$$
Re z = x,quad Im z = y. nonumber
$$
Если (x= 0), то есть (z = iy), то такое комплексное число называют чисто мнимым.
Здесь и всюду в дальнейшем, если не оговорено противное, в записи (x+iy) числа (x) и (y) считаются действительными (вещественными).
Число (displaystylesqrt{x^2+y^2}) обозначают (|z|) и называют модулем комплексного числа (z), то есть
$$
|z|=|x + iy|=sqrt{x^2+y^2}.label{ref4}
$$
Заметим, что (|z|geq 0) и ({|z| = 0}Leftrightarrow {z=0}).
Комплексное число (x-iy) называют сопряженным комплексному числу (z = x + iy) и обозначают (overline{z}) то есть
$$
overline{z} = overline{x+iy}= x-iy.label{ref5}
$$
Из равенств eqref{ref4} и eqref{ref5} следует, что
$$
|z| = |overline{z}|,qquad zoverline{z}=|z|^2,label{ref6}
$$
так как (zoverline{z}=(x+iy)(x-iy) = x^2 + y^2).
Свойства операций.
Операции сложения и умножения комплексных чисел обладают свойствами:
- коммутативности, то есть
$$
z_1+z_2=z_2+z_1,qquad z_1z_2=z_2z_1;nonumber
$$ - ассоциативности, то есть
$$
(z_1+z_2)+z_3= z_1 + (z_2+z_3),qquad (z_1z_2)z_3=z_1(z_2z_3);nonumber
$$ - дистрибутивности, то есть
$$
z_1(z_2 + z_3) = z_1z_2+z_1z_3.nonumber
$$
Эти свойства вытекают из определения операций сложения и умножения комплексных чисел и свойств операций для вещественных чисел.
Из этих свойств следует, что сложение и умножение комплексных чисел можно выполнять по правилам действий с многочленами, заменяя (i) на (-1). Например, равенство eqref{ref2} можно получить так:
$$
z_1z_2=(x_1+iy_1)(x_2+iy_2)=\=x_1 x_2+i x_1 y_2+ix_2 y_1+i^2 y_1 y_2=x_1x_2-y_1y_2+i(x_1 y_2+x_2 y_1).nonumber
$$
Множество комплексных чисел обозначают буквой (mathbb{C}). Числа (0= 0 + 0cdot i) и (1 = 1 + 0cdot i) на множестве (mathbb{C}) обладают такими же свойствами, какие они имеют на множестве (mathbb{R}), а именно: для любого (z in mathbb{C}) справедливы равенства
$$
z+ 0 = z,qquad zcdot 1 = z.nonumber
$$
На множестве (mathbb{C}) вычитание вводится как операция, обратная сложению. Для любых комплексных чисел (z_1=_1+iy_1) и (z_2 = x_2 + iy_2) существует, и притом только одно, число (z) такое, что
$$
z+z_2=z_1.label{ref7}
$$
Это число называют разностью чисел (z_1) и (z_2) и обозначают (z_1-z_2). В частности, разность (0 -z) обозначают (-z).
Из уравнения eqref{ref7} в силу правила равенства и определения суммы комплексных чисел следует, что
$$
z_1-z_2=(x_1-x_2)+i(y_1-y_2).nonumber
$$
Деление на множестве (mathbb{C}) вводится как операция, обратная умножению, а частным от деления комплексного числа (z_1=_1+iy_1) на число (z_2 = x_2 + iy_2) называют такое число (z), которое удовлетворяет уравнению
$$
zz_2=z_1label{ref8}
$$
и обозначается (z_1:z_2) или (displaystyle frac{z_1}{z_2}).
Докажем, что уравнение eqref{ref8} для любых комплексных чисел (z_1) и (z_2), где (z_2neq 0), имеет единственный корень.
(circ) Умножая обе части уравнения eqref{ref8} на (overline{z}_2), получим в силу равенства eqref{ref6} уравнение
$$
z|z_2|^2 = z_1overline{z}_2,label{ref9}
$$
которое равносильно уравнению eqref{ref8}, так как (overline{z}_2neq 0).
Умножая обе части eqref{ref9} на (displaystylefrac{1}{|z_2|^2}), получаем (z=displaystylefrac{z_1overline{z}_2}{|z_2|^2}), то есть
$$
frac{z_1}{z_2}=frac{z_1overline{z}_2}{|z_2|^2},nonumber
$$
или
$$
frac{z_1}{z_2}=frac{x_1+iy_1}{x_2+iy_2}=frac{(x_1+iy_1)(x_2-iy_2)}{x_2^2+y_2^2}=frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+ifrac{x_2y_1-x_1y_2}{x_2^2+y_2^2}. bulletnonumber
$$
Эту формулу можно не запоминать — важно знать, что она получается умножением числителя и знаменателя на число, сопряженное со знаменателем.
Пример 1.
Найти частное (displaystyle frac{z_1}{z_2}), если (z_1=5-2i, z_2=3 + 4i).
Решение.
$$
trianglequad frac{z_1}{z_2}=frac{(5-2i)(3-4i)}{(3+4i)(3-4i)}=frac{15-26i+8i^2}{25}=frac7{25}-frac{26}{25}i. blacktrianglenonumber
$$
Геометрическая интерпретация комплексного числа.
Комплексная плоскость.
Пусть на плоскости задана прямоугольная система координат. Комплексное число (z=x+iy) изображается точкой плоскости с координатами ((x,y)), и эта точка обозначается той же буквой (z).
Такое соответствие между множеством (mathbb{C}) и точками плоскости является взаимно однозначным: каждому числу (zinmathbb{C}) соответствует одна точка плоскости с координатами ((x,y)), и наоборот, каждой точке плоскости с координатами ((x,y)) соответствует одно комплексное число (z=x+iy). Поэтому слова “комплексное число” и “точка плоскости” часто употребляются как синонимы.
При этом действительные числа, то есть числа вида (x+0cdot i), изображаются точками оси абсцисс, а чисто мнимые числа, то есть числа вида (iy = 0 + iy) — точками оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат — мнимой осью. Плоскость, на которой изображаются комплексные числа, называют комплексной плоскостью.
На рис. 31.1 изображены точки (z, -z, overline{z}, -overline{z}). Отметим, что точки (z) и (-z) симметричны относительно точки (O), а точки (z) и (overline{z}) симметричны относительно действительной оси.
Геометрический смысл модуля комплексного числа.
Комплексное число (z=x+iy) можно изображать вектором с началом в точке (O) и концом в точке (z). Этот вектор будем обозначать той же буквой (z). Из рис. 31.1 или из формулы eqref{ref4} видно, что длина вектора (z) равна (|z|) и справедливы неравенства (|x|leq |z|, |y|leq |z|), то есть
$$
|Re z|leq |z|,quad |Im z|leq |z|.nonumber
$$
С помощью векторной интерпретации наглядно иллюстрируются сумма и разность комплексных чисел. Число (z_1+z_2) изображается вектором, построенным по правилу сложения векторов (z_1) и (z_2), а вектор (z_1-z_2) можно построить как сумму векторов (z_1) и (-z_2). Из рис. 31.2 видно, что расстояние между точками (z_1) и (z_2) равно длине вектора (z_1-z_2), то есть равно (|z_1-z_2|). Это же утверждение следует из равенства
$$
|z_1-z_2|=sqrt{(x_1-x_2)^2+(y_1-y_2)^2}.nonumber
$$
Итак, (|z_1-z_2|) — расстояние между точками (z_1) и (z_2).
Пример 2.
Дать геометрическое описание множества всех точек комплексной плоскости, удовлетворяющих условию:
- (|z-z_0| = R, R > 0);
- (1 < |z-1| < 2);
- (|z-i| = |z + i|).
Решение.
- (triangle) Условию (z-z_0=R), где (R > 0), (z_0) — заданное комплексное число, удовлетворяют все точки, расстояние от которых до точки (z_0) равно (R), то есть точки, лежащие на окружности радиуса (R) с центром в точке (z_0).
- Условию (|z-1| < 2) удовлетворяют все точки, лежащие внутри круга радиуса 2 с центром в точке (z = 1), а условию (|z-1| > 1) — точки, лежащие вне круга радиуса 1 с центром в точке (z = 1).
Оба эти условия выполняются для точек, лежащих между окружностями (|z-1| = 1) и (|z-1| = 2) (рис. 31.3). - Условию (|z-i| = |z + i|) удовлетворяют те и только те точки, которые равноудалены от точек (i) и (-i), то есть все точки действительной оси. (blacktriangle)
Покажем, что для любых комплексных чисел (z_1) и (z_2) справедливы неравенства
$$
||z_1|-|z_2||leq |z_1+z_2|leq |z_1|+|z_2|.label{ref10}
$$
(circ) Рассмотрим треугольник с вершинами (0, z_1) и (z_1+z_2) (рис. 31.2). Длины его сторон равны (|z_1|, |z_2|) и (|z_1+z_2|). Поэтому неравенства eqref{ref10} выражают известные из геометрии свойства длин сторон треугольника. (bullet)
Тригонометрическая и показательная формы комплексного числа.
Пусть (r) и (varphi) — полярные координаты точки (z = x + iy) комплексной плоскости (рис. 31.4); тогда
$$
x= rcosvarphi,quad y=rsinvarphi,label{ref11}
$$
где (r=displaystylesqrt{x^2+y^2}=|z|, varphi) — угол между действительной осью и вектором (z), отсчитываемый от положительного направления действительной оси. Если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке — отрицательной. Этот угол называют аргументом комплексного числа (z (zneq 0)) и обозначают (operatorname{arg}z). Для числа (z = 0) аргумент не определяется, поэтому в дальнейшем при использовании понятия аргумента предполагается, что (zneq 0).
Из равенств eqref{ref11} следует, что любое комплексное число (z = x + iy), где (zneq 0), представляется в виде
$$
z=r(cosvarphi+isinvarphi).label{ref12}
$$
Запись комплексного числа (zneq 0) в виде eqref{ref12} называют тригонометрической формой комплексного числа.
Из формул eqref{ref11} находим
$$
cosvarphi=frac{x}{sqrt{x^2+y^2}},qquad sinvarphi=frac{y}{sqrt{x^2+y^2}}.label{ref13}
$$
Решив систему eqref{ref13}, найдем аргумент комплексного числа (zneq 0). Эта система имеет бесконечно много решений вида (varphi= varphi_0+2kpi), где (kin mathbb{Z}), (varphi_0) — одно из решений системы eqref{ref13}, то есть аргумент комплексного числа определяется неоднозначно.
Для нахождения аргумента обычно пользуются не формулами eqref{ref13}, а формулой
$$
operatorname{tg}varphi=frac{y}{x},label{ref14}
$$
получаемой почленным делением второго из равенств eqref{ref13} на первое. Следует иметь в виду, что не все значения (varphi), удовлетворяющие уравнению eqref{ref14}, являются аргументами числа (z).
Пример 3.
Найти все аргументы числа (-1+isqrt{3}) и записать это число в тригонометрической форме.
Решение.
(triangle) Комплексное число лежит во второй четверти, поэтому в качестве одного из решений уравнения (operatorname{tg}varphi = -sqrt{3}) можно взять (varphi_0=displaystylefrac{2pi}{3}), а все значения аргумента данного комплексного числа определяются формулой
$$
varphi= frac{2pi}{3}+2pi k,quad kinmathbb{Z}.nonumber
$$
Так как (|-1+isqrt{3}|=2), то
$$
-1+isqrt{3}=2left(cosfrac{2pi}{3}+isinfrac{2pi}{3}right).quad blacktriangle
$$
Если (|z|=1, varphi=operatorname{arg}z), то из формулы eqref{ref12} получаем (z=cosvarphi+isinvarphi). Комплексное число (cosvarphi+isinvarphi) обозначают символом (e^{ivarphi}), то есть для любого (varphiinmathbb{R}) функция (e^{ivarphi}) определяется формулой Эйлера
$$
e^{ivarphi}=cosvarphi+isinvarphi.label{ref15}
$$
Равенство eqref{ref15} находит свое обоснование в теории рядов.
Из формулы eqref{ref15} следует, что (e^{2pi i}=1, e^{pi i}=-1, e^{pi i/2}=i, e^{-pi i/2}=-i) (рис. 31.5) и (|e^{ivarphi}|=1) для любого (varphiinmathbb{R}).
Заменяя в равенстве eqref{ref15} (varphi) на (-varphi), получаем
$$
e^{-ivarphi}=cosvarphi-isinvarphi,label{ref16}
$$
а из равенств eqref{ref15} и eqref{ref16} следует, что
$$
cosvarphi=frac{1}{2}(e^{ivarphi}+e^{-ivarphi}),qquad sinvarphi=frac{1}{2i}(e^{ivarphi}-e^{-ivarphi}).label{ref17}
$$
Отметим, что
$$
e^{ivarphi_1}e^{ivarphi_2}=e^{i(varphi_1+varphi_2)},qquad frac{e^{ivarphi_1}}{e^{ivarphi_2}}=e^{i(varphi_1-varphi_2)}.label{ref18}
$$
Для доказательства формул eqref{ref18} следует воспользоваться формулами eqref{ref15} и eqref{ref2}, а также формулами синуса и косинуса суммы (разности) углов. С помощью индукции из eqref{ref18} можно получить формулу Муавра
$$
e^{invarphi}=(cosvarphi+isinvarphi)^n=cos nvarphi+isin nvarphi,qquad nin mathbb{N}.nonumber
$$
Используя формулы eqref{ref12} и eqref{ref15}, запишем комплексное число (zneq 0) в показательной форме
$$
z = re^{ivarpi},quad r=|r|,quad varphi=operatorname{arg}z.label{ref19}
$$
С помощью равенств eqref{ref18} можно получить формулы для произведения и частного комплексных чисел: если (z_1=r_1 e^{ivarphi_1}, z_2=r_2 e^{ivarphi_2}), то
$$
z_1z_2=r_1r_2e^{i(varphi_1+varphi_2)},label{ref20}
$$
$$
frac{z_1}{z_2}=frac{r_1}{r_2}e^{i(varphi_1-varphi_2)},quad z_2neq 0.label{ref21}
$$
Из формулы eqref{ref20} следует, что при перемножении комплексных чисел их модули перемножаются, а аргументы складываются, то есть
$$
begin{array}{c}vert z_1z_2vert=vert z_1vertcdotvert z_2vert,\varphi_1+varphi_2=arg(z_1+z_2),end{array}nonumber
$$
если (varphi_1=operatorname{arg}z_1, varphi_2=operatorname{arg}z_2).
Аналогично из формулы eqref{ref21} следует, что модуль частного двух комплексных чисел равен частному модулей этих чисел, а разность аргументов делимого и делителя является аргументом частного, то есть
$$
left|frac{z_1}{z_2}right|=frac{|z_1|}{|z_2|},qquad z_2neq 0,nonumber
$$
и
$$
varphi_1-varphi_2=operatorname{arg}frac{z_1}{z_2},nonumber
$$
если (varphi_1=operatorname{arg}z_1, varphi_2=operatorname{arg}z_2).
Пример 4.
Вычислить (displaystylefrac{(1+i)^4}{(1-isqrt{3})^6}).
Решение.
(triangle) Так как
$$
1+i=sqrt{2}e^{ipi/4},qquad 1-isqrt{3}=2e^{-ipi/3},nonumber
$$
то
$$
frac{(1+i)^4}{(1-isqrt{3})^6}=frac{(sqrt{2})4 e^{ipi}}{2^6 e^{-2pi i}}=-frac{1}{16}. blacktrianglenonumber
$$
Из геометрической интерпретации (рис. 31.4) следует правило равенства двух комплексных чисел в показательной форме: если (z_1=r_1 e^{ivarphi_1}) и (z_2 = r_2 e^{ivarphi_2}), то (z_1=z_2) тогда и только тогда, когда
$$
r_1=r_2,qquad varphi_1=varphi_2+2kpi,quad kin mathbb{Z}.nonumber
$$
Рассмотрим теперь некоторые важные свойства комплексно сопряженных чисел. Пусть (z = re^{ivarphi} = rcosvarphi + irsinvarphi), тогда (overline{z} = rcosvarphi-irsinvarphi = re^{-ivarphi}), т.e. если (varphi = operatorname{arg}z), то (-varphi=operatorname{arg}overline{z}). Отсюда и из равенств eqref{ref20}, eqref{ref21} следует, что
$$
overline{z_1z_2}=overline{z_1}overline{z_2},quad overline{left(frac{z_1}{z_2}right)}=frac{overline{z_1}}{overline{z_2}},quad overline{(z^n)}=(overline{z})^n,quad nin mathbb{N},nonumber
$$
а из определения комплексно сопряженного числа следует, что
$$
overline{z_1+z_2}=overline{z_1}+overline{z_2},quad overline{z_1-z_2}=overline{z_1}-overline{z_2}.
$$
Извлечение корня.
Рассмотрим уравнение
$$
z^n=a,label{ref22}
$$
где (aneq 0) — комплексное число, (n) — натуральное число.
Если (z=re^{ivarphi}, a=rho e^{itheta}), то уравнение eqref{ref22} примет вид
$$
r^n e^{invarphi}=rho e^{itheta},nonumber
$$
откуда
$$
r^n=rho,quad nvarphi=theta+2kpi,quad kinmathbb{Z},nonumber
$$
и поэтому
$$
r=sqrt[n]{rho},qquad varphi_k=frac{1}{n}(theta+2kpi),quad kin mathbb{Z},label{ref23}
$$
то есть числа
$$
z_k=sqrt[n]{rho}e^{ivarphi_k}label{ref24}
$$
являются корнями уравнения eqref{ref22} и других корней это уравнение не имеет.
Заметим, что числа (z_0, z_1, …, z_{n-1}) различны, так как их аргументы (displaystylevarphi_0=frac{theta}{n}, varphi_1=frac{theta}{n}+frac{2pi}{n}, …, varphi_{n-1}=frac{theta}{n}+frac{2pi(n-1)}{n}) различны и отличаются друг от друга меньше, чем на (2pi). Далее, (z_n = z_0), так как (|z_n| = |z_0|=displaystylesqrt[n]{rho}) и (varphi_n=varphi_0+2pi). Аналогично, (z_{n+1} = z_1, z_{-1} = z_{n-1}) и т. д.
Итак, при (aneq 0) уравнение eqref{ref22} имеет ровно (n) различных корней, определяемых формулами eqref{ref23} и eqref{ref24}, где (k=0,1,…,n-1).
На комплексной плоскости точки (z_k (k=overline{0,n-1})) располагаются в вершинах правильного (n)-угольника, вписанного в окружность радиуса (displaystyle sqrt[n]{rho}) с центром в точке 0.
Пример 5.
Найти все корни уравнения (z^4 = 1 + i).
Решение.
(triangle) Корни (z_k (k = overline{0,3})) этого уравнения определяются формулами eqref{ref23} и eqref{ref24}, где (displaystyle rho=|1 + i| =sqrt{2}, theta=frac{pi}{4}), то есть
$$
z_k=sqrt[8]{2}e^{ivarphi_k},nonumber
$$
где
$$
varphi_k=frac{pi}{16}+frac{pi k}{2},quad k=0,1,2,3.nonumber
$$
Точки (z_k) располагаются в вершинах квадрата (рис. 31.6). (blacktriangle)
Комплекснозначные функции действительного переменного.
Если каждому значению (tin [alpha,beta]) поставлено в соответствие комплексное число (z=z(t)), то говорят, что на отрезке ([alpha,beta]) задана комплекснозначная функция действительного переменного.
Пусть (operatorname{Re}z(t) = x(t), operatorname{Im}z(t) = y(t)), тогда (z(t) = x(t)+iy(t)). Функцию (z(t)) можно рассматривать как вектор-функцию (z(t)=(x(t),y(t))). Определения предела, непрерывности, производной для комплекснозначной функции аналогичны соответствующим определениям для вектор-функции.
Например, производная функции (z(t) = x(t) + iy(t)) определяется формулой
$$
z'(t) = x'(t) + iy'(t).label{ref25}
$$
Следовательно, производная (z'(t)) существует, если существуют производные (x'(t)) и (y'(t)).
Применяя формулу eqref{ref25} к функции (e^{it}=cos t+isin t), получаем ((e^{it})’=-sin t+icos t=i^2sin t + icos t = i(cos t + isin t)), то есть
$$
(e^{it})’=i e^{it}.label{ref26}
$$
Таким образом, формула для производной комплексной функции (e^{it}) имеет такой же вид, как и для функции (e^{alpha t}), где (alphainmathbb{R}).
Определим теперь показательную функцию (displaystyle e^{(alpha+ibeta)t}), где (alpha,beta) — заданные действительные числа, (t) — действительное переменное. Функция (f(t) = e^t), где (tinmathbb{R}), удовлетворяет условию
$$
f(t_1)f(t_2) = f(t_1+t_2).label{ref27}
$$
Аналогично функция (e^{ibeta t}), где (betainmathbb{R}), обладает свойством eqref{ref27} в силу первого из равенств eqref{ref18}.
Поэтому функцию (e^{(alpha+ibeta)t}) естественно определить так, чтобы для нее выполнялось условие eqref{ref27}, то есть
$$
e^{(alpha+ibeta)t}=e^{alpha t}e^{ibeta t}.nonumber
$$
Используя формулу eqref{ref15}, отсюда находим
$$
e^{(alpha+ibeta)t} = e^{alpha t} (cos beta t+isinbeta t).label{ref28}
$$
Применяя к функции (e^{lambda t}), где (lambda=alpha+ibeta), правило дифференцирования eqref{ref25}, легко показать, что
$$
(e^{lambda t})=lambda e^{lambda t},quad lambda=alpha+ibeta.label{ref29}
$$
По аналогии с производной неопределенный интеграл от комплекснозначной функции (z(t)=x(t)+iy(t)) определяется формулой
$$
int z(t) dt = int x(t) dt + iint y(t) dt.nonumber
$$
Если комплексная функция (omega(t) = xi(t) + ieta (t)) такова, что (omega'(t)=z(t)), то
$$
int z(t)=int omega'(t)dt=int xi'(t)dt+iint eta'(t)dt = xi(t) + C_1 + ieta(t)+iC_2.nonumber
$$
Следовательно,
$$
int z(t) dt = omega(t) + C,quad C = C_1+iC_2.nonumber
$$
Применяя это утверждение к функции (e^{(alpha+ibeta)t}) и используя формулу eqref{ref29}, получаем
$$
int e^{(alpha+ibeta)t}=displaystyle frac{e^{(alpha+ibeta)t}}{alpha+ibeta}+C_1+iC_2.label{ref30}
$$
Выделяя в равенстве eqref{ref30} действительные и мнимые части, находим
$$
int e^{alpha t}cosbeta t dt + iint e^{alpha t}sinbeta t dt = frac{alpha-ibeta}{alpha^2+beta^2}e^{alpha t}(cosbeta t+isinbeta t)+C_1+C_2,nonumber
$$
откуда получаем
$$
int e^{alpha t}cosbeta t dt=frac{e^{alpha t}}{alpha^2+beta^2}(alphacosbeta t+betasinbeta t)+C_1,label{ref31}
$$
$$
int e^{alpha t}sinbeta t dt=frac{e^{alpha t}}{alpha^2+beta^2}(alphasinbeta t-betacosbeta t)+C_2,label{ref32}
$$
Заметим, что формула eqref{ref31} была получена с помощью интегрирования по частям в решенном ранее примере.
комплексный
- комплексный
- ко́мплексный
-
преставляющий собой комплекс чего-л., охватывающий группу предметов, явлений, процессов и т.д.
к-ные соединения — вещества получаемые сочетанием двух или более простых хим. соединений, напр. при действии аммиака NH4 на сульфат меди CUSO4 образуется комплексное соединение (CU(NH3)4)SO4;
к-ые соединения примен. для выделения и очистки золота, серебра, платиновых металлов, для получения многих других элементов и соединений высокой степени чистоты; природные к-ые соединения играют огромную роль в процессах дыхания, фотосинтеза и др.;
к-ые числа — числа вида a + bi, где а и b — действительные числа, a i — т. наз. мнимая единица (число, квадрат которого равен -1);
к-ая бригада — производственная бригада, организуемая из рабочих разных профессий для выполнения комплекса технологически разнородных работ, объединяемых общностью предмета труда или орудия труда.
- комплексный
-
[< лат.; см. комплекс] – соединённый с чем-либо, сложный; комплексные числа – числа вида а + bi, где а и b – обычные действительные числа, а i – так называемая мнимая единица, квадрат которой равен –1.
Новый словарь иностранных слов.- by EdwART, ,
2009.
Большой словарь иностранных слов.- Издательство «ИДДК»,
2007.
.
Смотреть что такое «комплексный» в других словарях:
-
КОМПЛЕКСНЫЙ — КОМПЛЕКСНЫЙ, комплексная, комплексное (книжн.). прил. к комплекс. Комплексное соединение (хим.). Комплексный метод преподавания. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
-
комплексный — единый, систёмный, систематический, систематичный, планомерный, целостный, неделимый, монолитный; сопряженный, комплектный, мнимый, совокупный Словарь русских синонимов. комплексный прил., кол во синонимов: 4 • комплектный (9) … Словарь синонимов
-
комплексный — КОМПЛЕКС, а, м. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
-
комплексный — представляющий собою комплекс чего либо; охватывающий группу объектов, явлений, процессов и пр. Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998 … Большая психологическая энциклопедия
-
КОМПЛЕКСНЫЙ — [см. комплекс] прил. от сл. комплекс; представляющий собой комплекс чего л.; охватывающий группу предметов, явлений, процессов (напр., К. подход к диагностике и преодолению двигательных нарушений; см. Комплексный подход к человеку) … Психомоторика: cловарь-справочник
-
Комплексный компонент измерительной системы — (по ГОСТ Р 8.596) конструктивно объединенная или территориально локализованная совокупность компонентов, составляющая часть измерительной системы, завершающая, как правило, измерительные преобразования, вычислительные и логические операции,… … Словарь-справочник терминов нормативно-технической документации
-
Комплексный книготорговый индекс-шифр — Комплексный книготорговый индекс шифр стандартный элемент выходных сведений, предназначенный для классификации книги в книготорговой сети (книжных магазинах и т. д.). Он применялся в выходных сведениях изданий СССР и России до… … Википедия
-
Комплексный подход к проблеме равенства полов — (комплексный подход к проблеме равенства между женщинами и мужчинами) это стратегия, заключающаяся во внедрении проблематики равенства полов на все уровни общества посредством организации системы ее учета при принятии политических решений.… … Термины гендерных исследований
-
комплексный показатель качества продукции — Показатель качества продукции, характеризующий несколько ее свойств. [ГОСТ 15467 79] Пояснения Примерами единичных показателей качества продукции могут служить: наработка радиоприемника на отказ; интенсивность отказов резистора; калорийность… … Справочник технического переводчика
-
Комплексный и Комплексный — прил. 1. Представляющий собою комплекс (1) чего л.; охватывающий целую группу предметов, явлений, процессов и т.п Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Все словари русского языка: Толковый словарь, Словарь синонимов, Словарь антонимов, Энциклопедический словарь, Академический словарь, Словарь существительных, Поговорки, Словарь русского арго, Орфографический словарь, Словарь ударений, Трудности произношения и ударения, Формы слов, Синонимы, Тезаурус русской деловой лексики, Морфемно-орфографический словарь, Этимология, Этимологический словарь, Грамматический словарь, Идеография, Пословицы и поговорки, Этимологический словарь русского языка.
комплексное число
Энциклопедический словарь
Ко́мпле́ксное число́ — число вида х + iy, где х и у — действительные числа, а i — так называемая мнимая единица (число, квадрат которого равен -1); х называется действительной частью, а у — мнимой частью комплексного числа. Действительные числа — частный случай комплексного числа (при у = 0). Комплексные числа, не являющиеся действительными (у ≠ 0), иногда называются мнимыми числами, при х = 0 комплексные числа называются чисто мнимыми. Геометрически каждое комплексное число х + iy изображается точкой плоскости, имеющей прямоугольные координаты х и у (см. рис.). Если полярные координаты этой точки обозначить через r и φ, то соответствующее комплексное число можно представить в виде: r(cosφ + isinφ) (тригонометрическая форма комплексного числа), 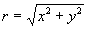
* * *
КОМПЛЕКСНОЕ ЧИСЛО — КО́МПЛЕ́КСНОЕ ЧИСЛО́, число вида x + iy, где х и y — действительные числа, а i — т. н. мнимая единица (число, квадрат которого равен -1); х называется действительной частью, а y — мнимой частью комплексного числа. Действительные числа — частный случай комплексных чисел (при y = 0). Комплексные числа, не являющиеся действительными (y № 0), иногда называются мнимыми числами, при х = 0 комплексные числа называются чисто мнимыми. Геометрически каждое комплексное число x + iy изображается точкой плоскости, имеющей прямоугольные координаты х и y. Если полярные координаты этой точки обозначить через r и j, то соответствующее комплексное число можно представить в виде: r (cosj+i sinj) (тригонометрическая форма комплексного числа); называется модулем комплексного числа x+iy, а = j — arctg(y/x) его аргументом, или в экспоненциальном виде: r eij
Большой энциклопедический словарь
КОМПЛЕКСНОЕ число — число вида x + iy, где х и y — действительные числа, а i — т. н. мнимая единица (число, квадрат которого равен ?1); х называется действительной частью, а y — мнимой частью комплексного числа. Действительные числа — частный случай комплексных чисел (при y = 0). Комплексные числа, не являющиеся действительными (y ? 0), иногда называются мнимыми числами, при х = 0 комплексные числа называются чисто мнимыми. Геометрически каждое комплексное число x + iy изображается точкой плоскости, имеющей прямоугольные координаты х и y. Если полярные координаты этой точки обозначить через r и ?, то соответствующее комплексное число можно представить в виде: r (cos?+i sin?) (тригонометрическая форма комплексного числа); называется модулем комплексного числа x+iy, а = ? ? arctg(y/x) его аргументом, или в экспоненциальном виде: r ei?
Идеография
▲ число
комплексное число.
мнимое число — результат извлечения корня.
тензор (# инерции. # диэлектрической проницаемости).
тензорный.
спинор. | гиперкомплексные числа.
кватернион.
↓ вектор
Полезные сервисы
Содержание
- 1 Русский
- 1.1 Тип и синтаксические свойства сочетания
- 1.2 Произношение
- 1.3 Семантические свойства
- 1.3.1 Значение
- 1.3.2 Синонимы
- 1.3.3 Антонимы
- 1.3.4 Гиперонимы
- 1.3.5 Гипонимы
- 1.4 Этимология
- 1.5 Перевод
- 1.6 Библиография
Русский[править]
Тип и синтаксические свойства сочетания[править]
ко́мп—лекс—но·е чис—ло́
Устойчивое сочетание (термин). Используется в качестве именной группы.
В профессиональной речи математиков — комп—ле́кс—но·е чис—ло́
Произношение[править]
- МФА: [ˈkomplʲɪksnəɪ̯ə t͡ɕɪˈsɫo]
Семантические свойства[править]
Значение[править]
- матем. число, состоящее из действительной и мнимой части ◆ Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица, то есть одно из чисел, удовлетворяющих уравнению i2 «равно» -1. ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
- вещественное число
Гиперонимы[править]
- число
Гипонимы[править]
Этимология[править]
Перевод[править]
| Список переводов | |
|
Библиография[править]
|
|
Статья нуждается в доработке.
Это незаконченная статья. Вы можете помочь проекту, исправив и дополнив её.
(См. Общепринятые правила). |